非正交晶胞正交化方法

最近在处理的结构的时候，本来是正交的晶胞，由于我切了某个面以后，变成了非正交的了（比如说a和b并不垂直，但是c还是垂直于ab构成的平面）。懒人做法当然是上网搜教程啦~~~~，这里的内容我是从b站学习来的，有兴趣可以去原地址看视频：BV16a4y1R7qB，在B站搜索即可，我也是学习原视频学来的。

其实方法非常简单。比如说POSCAR文件，我们仅仅讨论两个不垂直的晶格矢量a和b:

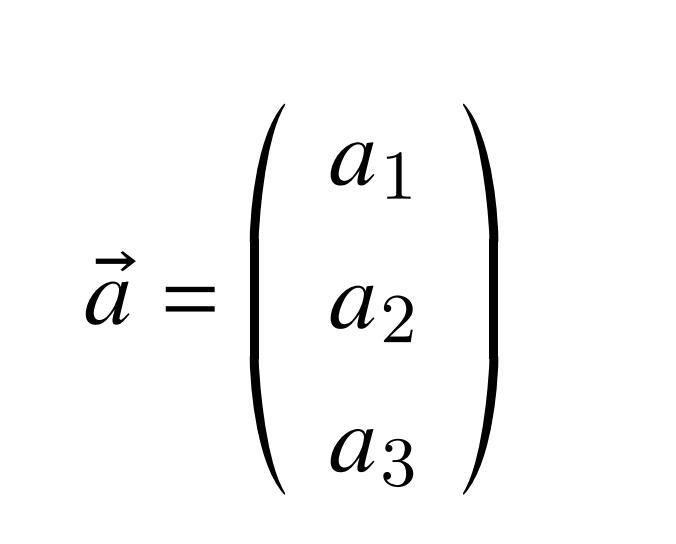
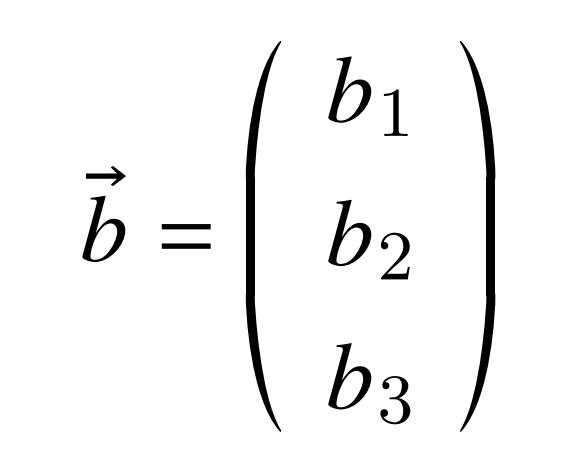
这时需要考虑的是，是否存在一个线性变换，使得这两个矢量a和b可以正交。

正交的条件非常好定，只需要两个矢量a和b的余弦值为0即可（在计算机中，可以设置一个非常小的值代替0），我们现在得到条件1：

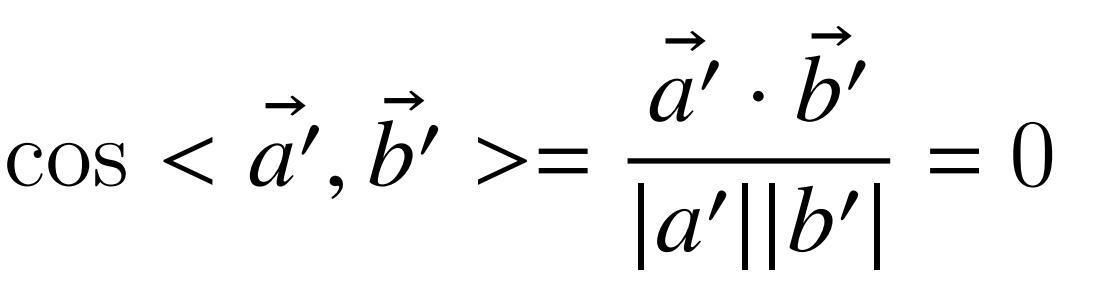
再来看看条件2。对于晶体而言，最重要的就是周期性条件，再结合一下对于POSCAR中3个矢量的理解。不难得到，变换矩阵的4个值都必须为整数，我们得到条件2：

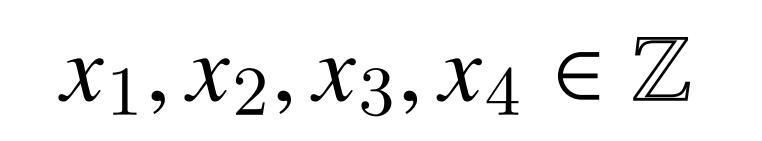
接下来就是另一个问题，我们建系是在右手系下建立的，那么在变换以后也必须满足右手系。由行列式公式：

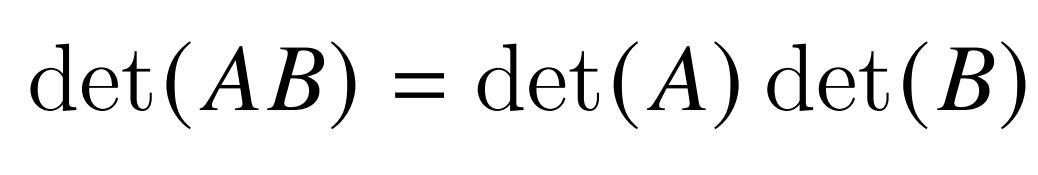
我们可以知道，要想保证变换后的两个矢量和c 满足右手系，这只需要这个变换矩阵的行列式为正的即可，我们得到条件3：

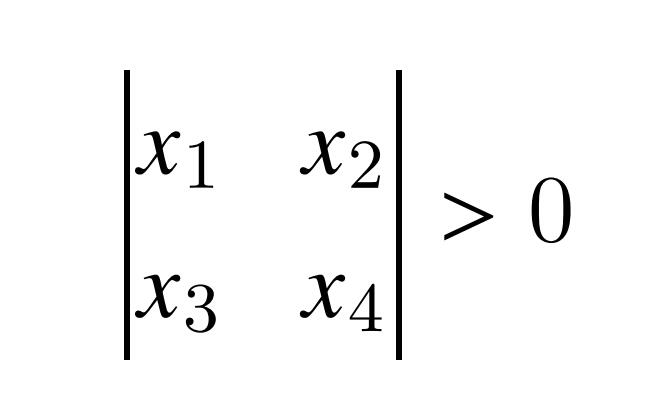
好了，我们已经得到这个矩阵的所有约束条件了，但是还缺一个最小化的条件4：

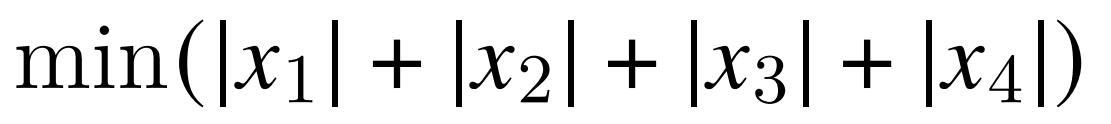
这样一来，我们就可以通过这样一个非线性规划问题（我没学过什么算法啊，这算是非线性规划还是线性规划啊。。。。。？？？？？？），得出来我们想要的这个矩阵。对于计算机求解，看似有点困难。但是非常幸运的是，这个矩阵中的4个数字都是整数，这样一来我们可以使用嵌套循环的方式就可以轻松解决这个问题啦！下面附Fortran代码：

module fun
implicit none
contains
real(kind=8) function cosin(a,b)
        real,dimension(3) :: a,b
        real :: temp1,temp2
        temp1=sqrt(a(1)**2+a(2)**2+a(3)**2)
        temp2=sqrt(b(1)**2+b(2)**2+b(3)**2)
        cosin=(a(1)*b(1)+a(2)*b(2)+a(3)*b(3))/(temp1*temp2)
end function cosin

real(kind=8) function cross(a,b)
        real,dimension(3) :: a,b
        cross=a(1)*b(2)-a(2)*b(1)
end function cross
end module fun
program nonlinear
        use fun
implicit none
integer :: x1,x2,x3,x4,s1,s2,s3,s4
integer :: i,j,k,l,m,n
integer :: up,down,temp,min_val
real,dimension(3) :: a,b,a_prime,b_prime
real :: error
a(1)=0.0  !这里从左到右输入POSCAR中不正交向量a的第1列的值
a(2)=0.0  !这里从左到右输入POSCAR中不正交向量a的第2列的值
a(3)=0.0  !这里从左到右输入POSCAR中不正交向量a的第3列的值
b(1)=0.0  !这里从左到右输入POSCAR中不正交向量b的第1列的值
b(2)=0.0  !这里从左到右输入POSCAR中不正交向量b的第2列的值
b(3)=0.0  !这里从左到右输入POSCAR中不正交向量b的第3列的值

up=10  !变换矩阵中每个整数的搜索上限
down=-10  !变换矩阵中每个整数搜索下限
error=1e-4  !最终最小化允许的误差
min_val=1000000
loop1:do i=down,up
loop2:  do j=down,up
loop3:          do k=down,up
loop4:                  do l=down,up
                                if (i==0 .and. j==0) then
                                        cycle loop4
                                end if
                                if (k==0 .and. l==0) then
                                        cycle loop4
                                end if
                                x1=i
                                x2=j
                                x3=k
                                x4=l
                                if (x2*x3-x1*x4<0) then
                                        a_prime(1)=x1*a(1)+x2*b(1)
                                        a_prime(2)=x1*a(2)+x2*b(2)
                                        a_prime(3)=x1*a(3)+x2*b(3)
                                        b_prime(1)=x3*a(1)+x4*b(1)
                                        b_prime(2)=x3*a(2)+x4*b(2)
                                        b_prime(3)=x3*a(3)+x4*b(3)
                                        !write(*,*) abs(cosin(a_prime,b_prime))
                                        if (abs(cosin(a_prime,b_prime))<=error) then
                                                temp=abs(x1)+abs(x2)+abs(x3)+abs(x4)
                                                if (temp<min_val) then
                                                        min_val=temp

                                                        s1=x1
                                                        s2=x2
                                                        s3=x3
                                                        s4=x4
                                                end if
                                        end if
                                end if
                        end do loop4
                end do loop3
        end do loop2
end do loop1
write(*,*) s1,s2,s3,s4,min_val
stop
end program

别看套了4个循环，效率还可以。需要自己改误差参数以及矢量的分量值。输出的结果右4个数字，就是x1,x2,x3,x4的值，最后一个值是最小化的值，用来判断是否出错。

改完以后就可以用M某软件重新定义晶胞操作（具体可以Google一下怎么做），即可得到正交后的晶胞（但是不是立方，仅仅只能正交）。对于三个矢量都不垂直的情况，可以再探究探究。需要注意的是，重新定义后的正交晶胞的体积会变大，M某软件会提示你体积变大了多少倍，所以最后还要自己看情况调整。

最后最重要的是，任何变幻出来的正交胞，需要自己再三确认是否是原来的结构！！！！！！！！！！！！！！这非常重要，可以使用XRD辅助检验，一定要手动检查。

懒人最近的施工计划：

1. KNN最近邻算法

2. 基于高斯核函数的密度估计算法

3. 晶体空间群识别算法（这个论文还没看完捏~~）

就这样啦，拜拜~~~~